By John Jones, JD, PhD, Vaxxter contributor
Science in our daily life
With recent public announcements by Dr. Judy Mikovits and Dr. Dan Erickson, many of us know that something is wrong with the COVID models and something is wrong with the science. The gravamen of the debate has two foci: theory and data. And when it comes to questions of public health or any scientific claims, this should be where we put our attention.
Data without Theory is nonsense, and
Theory without Data is Poppycock
paraphrasing Dr. Tetyana Obukhanych (2013)
We are told that COVID-19 is contagious. What is the logic of the exogenous viral contagion theory? What is the data that supports or refutes it? Additionally, what is the logic and theory behind the purported health benefits of the lockdown? And, what data supports or refutes that theory?
When attempting to analyze the COVID-19, though we might acknowledge the complexity of having a multiplicity of variables. Variables such as reverse transcription from injected viruses and proteins, deficiencies of vitamin C, vitamin D3, selenium, exposure to 5G radiation, comorbidities, and more. The fundamental questions can be based on cause and effect.
In symbolic terms, we say that x causes y. As a mathematical equation, often used in statistics, the social sciences, and economics to explain any number of phenomena, we write y = a + bx + e. (Americans might be more familiar with the formula from high school algebra, y = mx + b). For our purposes, we must appreciate that these mathematical formulae, however, expressed, are what the epidemiologists call, the models.
An Exercise in Modeling and Deconstruction
The purpose of this article is to discuss the utility of modeling and to demonstrate how easy it is for “scientific” papers to make inane pronouncements when the authors don’t have to produce any model, adhere to principles of scientific inquiry or present sound statistical methodology.
In the past week, I was asked to analyze some publications from peer-reviewed journals that claim to show statistical evidence about the benefits of certain vaccines. The first, published in November 2017 in the Journal of Clinical and Infectious Disease, purports to detail the efficacy of Tdap for pregnant women. Pregnant women receive Tdap as a means to prevent pertussis in infants. See Skoff et al. 2017. The second paper was published in the January 2020 issue of the journal Vaccines. The paper claims that flu shots are good for you, but raises the risk that you’ll test positive for a coronavirus.
Though both papers purport to use statistical analysis and claim that certain statistical tests prove the efficacy and benefits of a given vaccine, as always, the devil is in the details. At the most superficial level, both papers fail to offer an equation that models a relationship between a cause (x) and an effect (y). Arguably this omission, this lack of simplicity, moves me to conclude that the papers are unscientific.
Yes, they have data. Yes, they present claims about statistical probabilities. But both publications lack methodological rigor and violate fundamental axioms of statistical modeling, making their conclusions invalid.
For the rest of this essay (part I), I will focus on the Tdap paper. Part II will examine the article about the influenza vaccine (Wolff 2020).
A Quick Detour: Some More Scientific Definitions
Among other things, two critical concepts and definitions must be clear in the world of falsifiable, positivistic science. They are reliability and validity. Measures are reliable or unreliable. (Synonyms for reliable include accurate or consistent). Everyday examples of devices that can provide reliable measures include a speedometer or a stopwatch.
Gray areas of measurement, instances with uncertainty and inconsistent determination, often come from the medical world. Examples include diagnoses for pneumonia, allergies, and/or hay fever. Though we are told today that typhoid fever and typhus are caused by different agents, in the 1800s, doctors routinely used the terms to describe what we would call the flu. No matter the cause, typhoid fever and typhus present with symptoms that are identical.
To claim that a theory is valid, is to declare two things:
- There is a logical connection between an independent variable (cause) and a dependent variable (outcome or result); and
- The relationship (the correlation) is a statistical certainty with a probability in excess of 95% or 99% – depending on the conventions of that field of science.
In sum, facts are reliable to the degree that they can be measured; and theories are valid to the degree that the facts are proven to be correlated.
Tdap for Mama? GSK says NO, but the CDC says YES!
In their paper on Tdap, Dr. Skoff and others (2017) insist that babies are less likely to suffer pertussis infection (by which the authors mean a diagnosis of whooping cough from a licensed medical practitioner) if the mother gets the Tdap shot during the third trimester of her pregnancy.
There is one big problem with the conclusion: ALL the babies in their sample (n = 775) had pertussis – whether the mothers were vaccinated (n = 494) or not (n = 281). Vaccinations occurred regardless of when the shot was received: before, during, or after the pregnancy. So that paper is not a study, it is not even a statistical evaluation. It is a mere report.
The Skoff et al. (2017) paper, was paid for by taxpayers across six states (California, New York, Oregon, Minnesota, New Mexico, and Connecticut). Tami Skoff, who started working at the CDC in 1999, led a team of 10 researchers. For some reason, they decided to construct an argument designed to convince pregnant women to get injected with either Boostrix (GSK) or Adacel (Sanofi).
That is, the team did not seek to answer the most important, simple question: “Will injecting women with Tdap affect the rate of pertussis infection in their babies?” That is how a truly scientific study would begin. It would ask a question and layout some hypotheses. Let’s always remember that the most significant hypothesis is the null hypothesis.
Null Hypothesis
As professor McDonald reminds us,
“The primary goal of a statistical test is to determine whether observed data, is different from what you would expect, [if] the null hypothesis [were true], that you should reject the null hypothesis.”
In order to craft the null hypothesis and any alternatives, we need to define the variables and operationalize them. Meaning, we need to determine how to measure the variables reliably. Skoff et al. (2017) defined the independent variable (x, mother received a Tdap vaccination), and scored that as Yes (1) or No (0).
Then they defined the dependent variable (y, baby who had pertussis) as:
“The onset of cough illness and at least one of the following:
(i) laboratory-confirmation (culture or PCR) of pertussis, epidemiological linkage to a laboratory-confirmed case; or
(ii) clinically-compatible illness (cough [at least] 2 weeks with paroxysms, inspiratory whoop or post-tussive vomiting) in an infant <2 months old.”
Now we can layout their implicit hypotheses:
H0 = Tdap vaccination status of the mother will not alter the rate of pertussis in their babies (that is x will have NO effect on y);
H1 = Tdap vaccination status of the mother will decrease the rate of pertussis in their babies (that is an increase in x will reduce y).
With a basic set of hypotheses and concrete parameters for the independent and dependent variables, we could construct a 2 X 2 table. Using these ideas, I present the data from Skoff et al. (2017) this way:
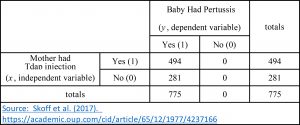
Perhaps you notice something curious? Despite compiling a list of 775 women and their babies, Skoff et al. (2017) examined no cases of children without pertussis. Nevertheless, they had the temerity to conclude:
“Vaccination [with Tdap] during pregnancy is an effective way to protect [sic] infants, during the early months of life.”
Where was the protection? The only infants they examined met their criteria for pertussis infection, and each incident started between day 15-45 of life – when the illness is life-threatening!
No Science Here – Just Faux Epidemiology
Obviously Skoff et al. (2017) did not conduct an experiment. They did not segregate women into a control and test group. They did not inject the control group with saline (a placebo) and inject others with Tdap. Instead, they used the idea of statistical control, which if done well, with proper sampling, could be used to evaluate valid hypotheses like those detailed above.
Routinely professors in sociology, political science, economics, and medicine use statistical control to evaluate hypotheses about cause and effect. The practice is valid, so long as the samples meet certain criteria, the least of which is variation within the variables.
So Skoff et al. (2017) did the first step. They divided two groups (test and control) according to the defined independent variable, the Tdap status of the mother. But for some reason, when it came to the dependent variable (the health of a baby), this team ignored a fundamental axiom of statistical tests: “variables must vary.” In this instance, the dependent variable (y, pertussis illness in an infant) had only one value, yes.
Normally, to investigate the relationship between two dichotomous variables, we could construct a 2 X 2 table, and apply a chi-square test. The purpose of the test is to evaluate the null hypothesis that “the relative proportions of one variable are independent of the second variable.” (McDonald 2014). (Often medical studies report an Odds-Ratio or Wald test, which is practically identical to the chi-square. I will discuss the use and limits of statistical tests employing the Odds-Ratio in part II).
Investigating Proportions
An honest investigation would want to know if the proportions in one variable (e.g., Tdap status of the mother) were the same for different values in the second variable (e.g., pertussis illness status in their infant).
Remember, real scientific inquiry assumes that any treatment, like a vaccine, or aspirin, or vitamin C has NO effect on the recipients – neither good nor bad. But as we have seen, since the 1950s, the dominant view is that there is no need to prove positive effects of vaccination. Additionally, it seems that practically all vaccine injuries are ignored as an impossibility, coincidence, or non-event.
Please recognize, Dr. McDonald does not label the two variables in a chi-square test as independent (x) and dependent (y). This is because the chi-square test does not presume to explain causality – rather it is a measure of correlation. After all, if there is no correlation, there is no causality. However, in reference to the Skoff et al. (2017) data set, I use the labels of independent and dependent because the vaccination event preceded the recorded illness of the child.
That said, for Skoff et al. (2017) an appropriate null hypothesis could have been articulated in this manner:
“The proportion of infants with pertussis, in vaccinated mothers, is equal to the proportion of sick infants in unvaccinated mothers.”
A real study would then calculate the proportion of sick children of the vaccinated and unvaccinated mothers – and compare the two. If the proportions were statistically significantly different (no matter which was higher or lower), we would reject the null hypothesis. Yet as their sample had no infants who did not have pertussis, the relative proportion of pertussis cases in babies, born either to vaccinated or to unvaccinated mothers, was the same: 100%!
Do shots make no difference?
In statistical terms, the data presented by Skoff et al. (2017) says that we cannot reject the null hypothesis that “the Tdap shot given to mothers, does not reduce pertussis in infants, under 2 months of age.” The only logical conclusion we can derive from this sample (n = 775), about pertussis illness in infants (y) and the Tdap status of the mothers (x), is that getting the shots makes no difference. Such is the very opposite of the conclusion Skoff et al. (2017) offer.
Obviously, we presume that this is not what occurs in the real world. We imagine that injecting a woman with Tdap, either before or during pregnancy, or post-partum and when she is breastfeeding, must have some impact on the baby. But the only way to use statistical analysis in order to reject the null hypothesis would be to have a random sample of infants whereby their scores for pertussis infection (the dependent variable) varied (included both yes = 1 and no = 0).
And Skoff et al. (2017) did not include those babies in their data.
Is it All Just Advertising?
Essentially what the Skoff study did was:
- looked at one outcome, “infants sick with pertussis”;
- parsed the time when the mother was injected with Tdap; and
- concluded that injection in the last stages of pregnancy reduces the probability that the child would be sick.
But how could they know? The had literally no basis of comparison. They also had no variation in their dependent variable.
I can only conclude that they wrote this paper to serve as a pseudo-scientific, medical advertisement for the Tdap vaccine. But was there a need to convince doctors, hospital administrators, and mothers to inject pregnant women with Tdap? Maybe so, if pregnant women and health care professionals are so foolish as to read the vaccine manufacturer’s package insert. Surely reading the vaccine insert would dissuade women and doctors from giving the shot to anyone!
GSK Warnings
Here is what GSK says about its Tdap shot:
Between 1-4% of all people experience serious adverse side-effects – including paralysis, heart attack, seizures, encephalitis, arthritis, and auto-immune disease. (See Boostrix package insert pages 10-13).
There is more from GSK. In Section 8, Use in Specific Populations, subsection 8.1. pregnant women, we read in part:
A developmental toxicity study has been performed in female rats … and revealed no evidence of harm to the fetus.
There are no adequate and well-controlled studies in pregnant women. Because animal reproduction studies are not always predictive of human response, BOOSTRIX should be given to a pregnant woman only if clearly needed.” (emphasis added).
And under Section 11, DESCRIPTION we see:
Each 0.5-mL dose contains aluminum hydroxide as adjuvant (not more than 0.39 mg aluminum by assay) … [no more than] 100 mcg of residual formaldehyde, and [no more than] 100 mcg of polysorbate 80 (Tween 80).
I guess Skoff and her 10 co-authors, the researchers, PhDs, lawyers, and marketing teams at GSK are putting women and babies at risk because they just do not know the science? Apparently, Skoff knows better. She would tell all women to get an injection of 390 micrograms of aluminum plus the formaldehyde and polysorbate 80, (the surfactant that enables the aluminum to enter the brain), preferably about three weeks before delivery.
Such advice from Skoff et al. (2017) is bewildering given that all the babies under evaluation in their review had pertussis anyway. That means, 494 women were told that a vaccine would help them and their babies by preventing pertussis, but instead, the women (and 139 babies) got blasted with aluminum. Regardless, these women watched their babies struggle with pertussis at the worst time, those critical first weeks of life.
Conclusions
Skoff et al. (2017) presented a review of 775 women and their sick babies. They crafted an arbitrary scale for what could have been an independent variable (Tdap injection) and created five sub-categories: no shot, pre-pregnancy, 1st or 2nd trimester, 3rd trimester, or post-partum.
Then they purported to offer a statistical analysis on the proportion of sick babies (n = 775) in relation to the category that they assigned to the mother. But as I noted above, without variation in both variables, there can be no true statistical test. Instead, Skoff et al. (2017) engaged in what is called a fishing expedition: They had no theory – but they had data.
They saw that the fewest number of sick babies were in their artificial category of “mothers who got the Tdap in the 3rd trimester.” But that mere association neither proves nor suggests that the vaccine provides any protection against pertussis. And because we had no variation in the dependent variable, we cannot see any pattern or trend – pro or con – from the Tdap vaccination.
Their report is not pseudo-science. It is not junk science. It was no science. We must reject it, and all studies like this, and demand better.
++++++++++++++++++++++++++++++++
 Like what you’re reading on Vaxxter.com?
Like what you’re reading on Vaxxter.com?
Share this article with your friends. Help us grow.
Join our list here or text MVI to 555888
++++++++++++++++++++++++++++++++
John C. Jones received his law degree (2001) and his Ph.D. is in political science (2003) from the University of Iowa. He has over 15 years of research and writing (both academic and journalistic) in fields of public policy and law, criminal and Constitutional law, and philosophy of science and medicine. His additional areas of expertise and specialized knowledge include applied statistics, etymology, political communications/public relations, litigation and court procedure. He has a particular interest in the science and history of vaccines.

